Frågor inför tentan

Jag har nu lagt ut på kurssidan den tentan som Mostafa gav i fjol. Som jag redan har betonat, ser mina tentor lite annorlunda ut. Min tenta kommer också att vara "öppen bok", så jag bifogar ingen formelsamling.

Det var få frågor vid föreläsningen idag, men jag har ny webcast onsdag 5 januari kl. 13:15.

God Jul!

Coolt!

Jag hittade en bok på nätet: Cool Thermodynamics av Gordon och Ng. Det är inte bara en cool titel, men det ser faktiskt ut som en trevlig bok om termodynamik. Ämnet är kylning - författarna kommer från Israel och från Singapore, det är begripligt att ämnet är av intresse för dem. Men på något sätt är det också coolare än värmemaskinerna som ångmaskiner, bilmotorer och strålturbiner. Boken är nog inte så bra för en grundkurs i termodynamik, man jag ska se om jag kan använda delar som övningsexempel eller tentaproblem.


Förresten, jag sade fel. Måndag 20 december är det föreläsning (eller problemlösning).

Värmetransport över irrvägar

Bilden ovan visar diffusion: för Brownsk rörelse av en partikel, av många partiklar och av ett enormt antal partiklar, till exempel sockermolekyler i en sockerlösning. Värmeledning sker i princip på samma sätt: diffusion av små energipaket ("fononer" i kristallina ämnen). (Skillnaden är att inte antalen energipaket är bevarade, utan bara den totala energin.)

Det är slumpvandring som gör att energikoncentrationen blir jämt fördelad, att entropin tilltar. Det kan inte hända (det är extremt osannolikt under universums livstid) att processen går att andra hållet, att energin av en stav fördelar sig så att den ena sidan av sig själv blir varmare än den andra sidan.

Om energikoncentrationen är proportionell mot temperatur (med andra ord: om man kan tala om en bestämd värmekapacitet), gör diffusionsmekanismen att Fouriers lag gäller: värmeflödet är proportionellt mot temperaturgradienten.

Om man tillämpar Fouriers lag och energibevarande på flödet in och ut en liten volymelement, leder det till en något mer komplicerad differentialekvation - värmeledningsekvationen, som är en form av diffusionsekvationen:

Temperaturändringen är alltså proportionell mot temperaturgradientens divergens (temperaturens Laplacian). I en dimension är det temperaturens andra derivata med hänseende till position. Om temperaturgradientens inte beror på position, är värmets inflöde lika stor som utflödet, och då är temperaturen konstant.

Ett exempel på hur värmefördelingen kan utveckla sig som funktion av tid:

Frågor och problem

Det här är stället för frågor och problem.

Konvektion och Newtons avsvalningslag

Ett av mekanismen för att jämna ut temperaturskillnader är konvektion. Det är värmetransport genom transport av varma fluider (gaser, vätskor). Eftersom densiteten beror på temperatur är sådana rörelser är oundvikliga i ett gravitationsfält - den lilla uppåtriktade kraften på varma volumelement räcker för att sätta igång cirkulation: den atmosfäriska cirkulationen och de mäktiga havsströmmarna, men även i en kastrull på spisen och i luften omkring våra kroppar. Om man vill påskynda nedkylning eller uppvärmning, använder man fläktar och pumpar.

Fysiken av konvektion är komplicerad, och ligger mer inom området fluiddynamik än inom termodynamik, men allmänt kan man säga att värmetransporten ökar med temperaturskillnaden. Newton var mer specifik och hans avsvalningslag säger att ändringen i temperatur är proportionell mot skillnaden i temperatur. Denna linjära approximation är ofta hyfsad bra när temperaturskillnaderna inte är för stora. Och den gäller förstås också för uppvärmningen av en kall kropp i en varm fluid.

Newtons avsvalningslag är egentligen en differentialekvation:

där K är någon konstant. Kolla att en lösning ges av formel (8.22) i boken:

som ger en exponentiellt avtagande temperatur med en karakteristisk tid tau = 1/K från en initial temperatur T_i vid t=0.



Man får samma tidsförlopp för andra fall där minskningen är proportionell mot beloppet, som till exempel vid radioaktivt sönderfall eller vid urladdning av en kondensator över ett elektriskt motstånd. I sådana elektriska kretsar gäller att tidskonstanten i sekund är lika med kondensatorns kapacitans i farad gånger det elektriska motståndet i ohm. På liknande sätt gäller vid avsvalning att tidskonstanten är proportionell mot kropppens värmekapacitet och mot värmemotståndet.

Boltzmannfaktorn

Boltzmannfaktorn används till exempel i halvledarfysik. Den säger att sannolikheten för exciterade tillstånd (av en elektron eller atom) är proportionell mot exp(-E/kT). Det är för mig otillfredsställande om sådant bara tas ur luften, särskilt när det finns en ganska enkel härledning från statistisk mekanik.

Betrakte ett litet två-nivå-system (E₁ och E₂) som är en del av ett stort system. Det lilla systemet är i termisk kontakt med resten, som fungerar som ett värmebad. När det lilla systemet ändrar energi, är ändringen i värmebadets temperatur T försumbar. Det är också så att dess energiändring E₁ - E₂ är infinitesimal (dE eller dU) i förhållande till badets totala energi. Men det påverkar badets multiplicitet Ω.

Om vi antilogaritmerar entropins definition, får vi Ω = exp(S/k). Från den statistiska definitionen för temperatur får vi dS = dU/T. Förhållandet av multipliciteterna för badet är Ω(E+dE)/Ω(E) = exp[(S(E+dE)-S(E))/k] = exp(dS/k) = exp(dE/kT) = exp((E₁ - E₂)/kT). Och det ger sannolikheterna för det lilla systemet, som är störst för grundtillståndet eftersom det ger badet störst multiplicitet. Badets multiplicitet växer exponentiellt med dess energi. Det är den enkla bakgrunden till Bolzmannfaktorn.

Van der Waals tillståndsekvation

Van der Waals föreslog 1873 i sin doktorsavhandling två korrektioner till allmännagaslagen: att ta hänsyn till molekylernas egen volym och att kompensera trycket för molekylernas attraktionskraft.

Ekvationen gav inte bara en bättre beskrivning av gasfasen vid högre tryck, utan den beskrev även kritisk punkt (upptäckt av Thomas Andrews, 1869) och fasövergången till vätska. För isotermer under en viss temperatur (den kritiska temperaturen) ser man av en pV-graf att det finns tre lösningar för volym för ett visst tryck. Det är klart att värdet med negativ kompressibilitet inte kan vara någon stabil lösning. Hur ska man då välja?

Så här kanske? Gasens tryck går upp vid volymminskning tills kompressibiliteten blir oändligt stor, för att då implodera till vätskans volym. Men... vad händer om man ökar volymen igen?

Maxwells lösning var att vid jämvikt måste integralen pdV från vätska till gas vara noll, att ytorna på båda sidor jämviktslinjen ska vara lika. Längs med linjen finns jämvikt mellan gas och vätska: en minskning av volymen gör att mängden vätska blir större, men trycket är konstant (mättnadstrycket för isotermens temperatur).

Fantastiska simuleringar

PhET har en massa interaktive simuleringar om fysik och om annat. Jag rekommenderar att ni lekar med dessa två. Det är helt fantastiskt att man kan köra molecular dynamics på det här sättet.


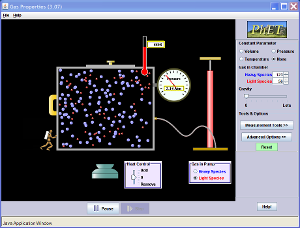
Den här handlar om gaser. Om man börjar med att vrida gravitation upp till max, pumpar in lite gas, och sedan kyler mer gasen till vanliga temperaturer, ser man vad som händer. Man kan öpnna behållarens lock, så att ibland en molekyl kan flyga iväg. Och man kan släppa ett lättare gas. Då förstår man varför jordens atmosfär inte har så mycket helium eller neon. Man kan förstås också köra utan gravitation, ändra volym, kolla gaslagar, osv.


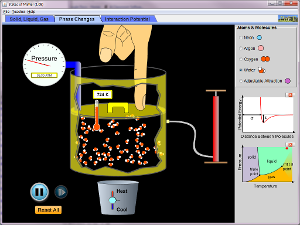
Det andra programmet här klarar av att simulera tillståndsekvationer och fasövergångar via simuleringar på ungefär jundra molekyler. Lite gravitation gör att kondenserad materia håller sig nära behållarens botten. En prick i fasdiagrammet visar vilket tillstånd beskrivs av programmet. Obs: akta att trycket inte får bli för högt - då smäller det!

Värmealstring

Kursboken heter ju Energilära. Men den handlar inte om alla former av energi. Bokens egentliga ämne är termodynamik. Sådana uthålliga energisystem som vattenkraftverk, vindkraft, solceller och bränsleceller lär man sig inte mycket om i den här kursen.

Och faktum är att en mycket stor del av vårt energibehov kommer från maskiner och motorer som fungerar på grund av skillnader i temperatur. Samma lagar som utvecklades för att analyserar verkningsgraden av ångmaskiner, tillämpas på kärnkraftverk och jetmotorer. Det är värmemaskiner, där något bränsle alstrar värme, som delvis konverteras till mekaniskt arbete.

Tabell 1.1 ger värmevärden för några bränslen. Enheterna är sådana som är av betydelse för elkraftsingenjörer. Kemister använder molära enheter, och då ger kol vid förbränning med syre ungefär 390 kJ/mol. En fysiker konverterar det till 4 eV per atom, det är enheter som i alla fall jag har lättare att relatera till.

Om man gör samma konvertering för bränslevärdet av uran i en bridreaktor, blir det 30 MeV per uranatom. Det är instruktivt att se var värmet kommer ifrån. En klyvning av en urankärna bör nämligen inte uppfattas som en kärnexplosion i miniatyr, som man lätt kan tro av skissar som den här:

Vad som egentligen händer är först att en infångad neutron gör att en urankärna blir två dotterkärnor nära intill varandra. Dessa repellerar varandra med Coulombkraften, som ger fragmenten stor kinetisk energi. Sedan bromsas fragmentens fart genom interaktion med elektroner och joner i materialet. Det är det som blir värme: oordnade vibrationer av atomer i material.

Samma sak sker också vid förbränning av kemiska bränslen. Vanligtvis sker reaktionen i gasfas. Efter en reaktion har molekylerna kinetiska energier på några eV, som genom stötar mot andra molekyler smetar ut till de oordnade rörelserna av en gas med hög temperatur.

Varför ger då en kärnreaktion många miljoner gånger större energi? Dat är för att avstånden är kortare och laddningarna större. När urankärnans "vätskedroppe" har blivit två, är det inbördes avståndet 10^-14 meter, tiotusen gånger mindre än storleken av atomer. Och laddningarna gör att den potentiella energin blir typ 40² gånger större. Tillsammans ger det kinetiska energier som är många miljoner gånger större.

E = m c² gäller i båda fallen.

Temperatur kan definieras!

Vi tror alla att vi vet vad temperatur är, att det är ungefär lika självklart som tid. Och visst kan vi titta hur mycket klockan är eller hur varmt det är, genom att kolla någon termometer eller klocka. Men vad är tid egentligen? Eller temperatur?

Temperatur var så självklar att termodynamiken hade glömt att ge en definition. Så det blev termodynamikens nollte huvudsats, att två kroppar som var för sig är i termisk jämvikt med en tredje kropp, står även i termisk jämvikt med varandra. Dessa har då samma temperatur. Temperatur är transitiv. Temperatur är en intensiv egenskap av ett system i jämvikt (inte extensiv, det vill säga proportionell mot hur stor systemet är). Och på 1700-talet utvecklade man termometerskalor.

Termometer i en bok av Linné från 1738

Nittonhundratalets termodynamik lyckades ge en absolut temperaturskala, genom att studera ideal gas och/eller med hjälp av termodynamiska resonemang om hur mycket mekaniskt energi man kunde få ur termisk energi vid vissa temperatursskillnader.

Men statistisk mekanik ger oss insikten att "samma temperatur" är det mest sannolika tillståndet i en precis statistisk mening. Att energi spontant flöder från system som har låg relativ ändring i antalet tillstånd (hög temperatur) till system med stor relativ ändring i antalet tillstånd vid en ändring i intern energi. Och att det är meningsfullt att definiera

Termisk jämvikt

Vi har sett att värme sprider ut sig i en spontan process. Men det var i samma material. När man har olika material, är inte en makroskopisk jämn energifördelning ett villkor för termisk jämvikt. Till exempel är vid 0 °C flytande vatten i jämvikt med is, fast energiinnehållet per molekyl i vatten är mycket högre än i is.

Det som karakteriserar jämviktstillståndet är att det är det mest sannolika tillståndet. Det makroskopiska tillståndet som är stabilt är det som har flest mikrotillstånd, som har störst Ω, som har den största multipliciteten. Vi har sett att Ω = Ω_A × Ω_B. När värmeenergi överförs från delsystem A till delsystem B, blir Ω_B större medan Ω_A minskar. Vad är då villkoret för att Ω för hela systemet ska vara maximal?

Det enklaste sättet att se det är att använda entropin. När Ω är maximal, är också dess logaritm S maximal. Derivatorna av S med avseende på energi måste vara lika. När det inträffar, finns ingen netto spontan energiöverföring mellan delsystemen. Det är termisk jämvikt. Och vi vet utav erfarenhet att det inträffar när delsystemen har samma temperatur.

Men vi kan också använda lite informell variationskalkyl. När Ω för systemet är maximal för överföring av en energimängd dq_A->B, är också produkten Ω_AΩ_B maximal:

Med regeln för derivata av produkt:

Värmet som tillförs delsystem A kommer från delsystem B, så vi kan skriva villkoret för jämvikt som:


Vilkoret för jämvikt är alltså att den relativa ändringen i antalet tillstånd är lika för båda delsystemen.

Även energi smetar ut

Olika tillstånd har man inte bara när positioner är olika, utan även när energier är olika. Som till exempel i animationen av det 2-dimensionella gaset som vi har tittat på. Kvantmekaniskt vet vi också att energinivåer av partiklar i lådor är kvantiserade, så att det inte är något konceptuellt problem med vad som räknas som olika tillstånd.

Kjellander tar som exempel fyra molekyler. Systemets energi kan vara koncentrerad till en molekyl, medan de tre andra befinner sig i grundtillståndet. Då finns det fyra olika mikrotillstånd som ser ut så. Eller samma mängd energi kan vara utsmetad över olika molekyler. Vid sådana tillstånd finns många fler mikrotillstånd, se Kjellander fig. 22. Sådana tillstånd är alltså mycket mer sannolika. Spontana processer och slumpvida ändringar gör att energin inte förblir koncentrerad till en molekyl, utan att den smetas ut över många.

Det stämmer också med med vår erfarenhet. På samma sätt som vi vet att en gas jämnar ut sig och att luften inte spontant kommer att befinna sig i norra delen av en föreläsningsssal, så vet vi också att energi sprider ut sig i spontana processer. Om vi tillför energi till någon kopparstav genom att värma upp den på ett ställe, kommer värmet att sprida sig genom diffusion (slumpvandring) tills stavens temperatur är lika överallt.

I alla vanliga system blir entropin högre när den interna energin är högre. Det är ocksa ofta så att antalet tillstånd tilltar med energi, till exempel i väteatomen.

Boltzmanns formel för entropi

I gyllene bokstäver på Boltzmanns grav:

Det skulle vara mer bekvämt med ett mått för antalet tillstånd av ett system som var additiv när man lägger ihop system. Ludwig Boltzmann gjorde det genom att ta logaritmen på Ω. Sedan finns det en konstant som gör att formeln stämmer med Clausius termodynamiska formel för entropi, men det tar vi senare.

Vi såg att antalet tillstånd är proportionell mot volymen upphöjd till antalet partiklar. Entropin är alltså proportionell mot antalet partiklar. Eller mera noggrant: det vi har visat är att entropiökningen är proportionell mot antalet partiklar.







Så om vi dubblerar volymen för de 47 partiklarna i figuren ovan, blir antalet tillstånd 2⁴⁷ gånger så stor, medan entropin ökar med 47 k_B ln 2, som är ett ganska litet belopp.

Att räkna Ω

För att kunna räkna på sannolikheterna för olika konfigurationer av ett system, måste man kunna räkna antalen tillstånd. Och vad är olika tillstånd? Räknas tillstånd som olika när någon atom förflyttat sig en pikometer? Eller om någon atom har en lite högre hastighet? I så fall skulle antalen tillstånd vara oändliga, och det skulle bli svårt att räkna dem.

Vi ska först räkna här med celler för positioner. Tillstånd räknas som olika när atomerna befinner sig i olika celler. Det är inte viktigt här hur stora cellerna är, men det finns en nedre gräns för vad som är en meningsfull storlek, och det är de-Broglie vånglängden. Här är figuren från Kellander för två partiklar som kan fördela sig över en volym som är uppdelad i sex celler:

Man ser att antalet tillstånd är 6×6=36. Allmänt gäller:

där N är antalet partiklar, V är totala volymen och v är volymen för en cell. Antalet tillstånd är alltså proportionellt mot volymen upphöjd till antalet partiklar.

Slumpmässiga rörelser

Animationen visar en 2-dimensionell gas av 32 skivor, kanske atomer som rör sig slumpmässig över en begränsad yta, instängda av fyra staket. För att lättare kunna fokusera blicken på en atom, är fem av dessa skivor markerade med röd färg. Rörelserna är slumpmässiga, förutom att animationen "loopar" efter ungefär 15 sekunder. Skivorna beter sig lite som biljardbollar, förutom att det inte finns någon friktion i modellen och det är helt elastiska stötar. Det gör att hastigheterna också är slumpmässiga.

Det finns en ruta där alla röda atomer finns i övre halvan. Chansen att det händer är ½ × ½ × ½ × ½ × ½ = 1/32, så det är inte osannolikt att det inträffar någon gång i 15 sekunder. Men sannolikheten att alla skivor någon gång skulle befinna sig i övre halvan är 1/2³² = 2,3 × 10^-10, mindre än en på en miljard. Det är klart att det inträffar om man väntar tillräckligt länge, men man får vänta 2²⁷ = 132 miljoner gånger längre - ungefär 60 år.

Då börjar man förstå man varför det "aldrig" händer att en mol gas befinner sig i ena halvan av en behållare. Universumets livstid är för kort för det. Och det beror inte på att molekylerna försöker undvika trängsel, utan bara på slumpen.

En annan början

Termodynamik är nog delen av fysik som jag gillar minst. Och nu ska jag för första gången undervisa i det. Det här kan vara min chans att äntligen lära mig lite känsla för de termodynamiska potentialerna. Boken "Energilära" håller en ganska trevlig nivå.

Men jag vill ta ett annat perspektiv. Här om någonstans är det viktigt att ta sin utgångspunkt i en "dynamisk partikelmodell", som det står i utkastet till grundskolans kursplan för fysik. Och det betyder att jag ska prata mindre om de termodynamiska relationerna som är viktiga för processingenjörer, och mer om statistisk fysik.

Det finns en annan bok på svenska: Vad är drivkraften i molekylernas värld? Det är en molekylär introduktion till termodynamik. Jag har inte tagit den som kursbok, bland annat för att den inte innehåller några övningsuppgiften. Och det är verkligen bara en introduktion till ämnet. Den är inte dyr och jag kan rekommendera alla att läsa den.

Så jag ska följa Roland Kjellander och börja kursen med begreppet entropi. Inte som Clausius (se sida 324 i Energilära), utan utifrån sannolikhetslära. Och jag hoppas att detta ska ge er en annan och större förståelse för alla de intressanta processerna som sker omkring oss och inuti oss.